Lecture 8
这节最重要的结论就是随机分配居然要比主动选择好!
终于解决了我心中多年的一些困惑。
Location model
有两个镇子:E, W, 每个镇子能够居住10w人。
有两种人:T, S,每个种类有10w人。
大家都要选择自己是居住E还是W。
大家都同时进行选择,并且一旦某个镇子选择的人数超过限制,那么就随机进行分配。
payoffs:
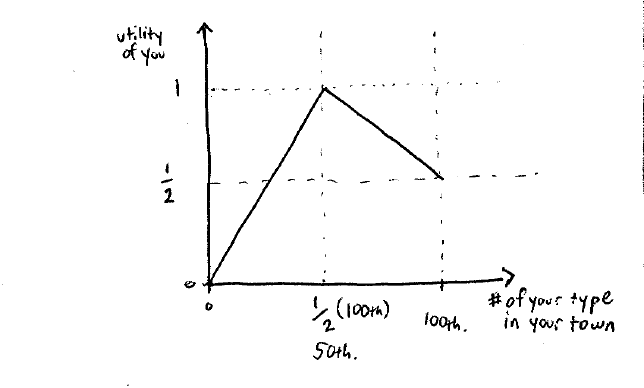
横轴表示和自己是在居住的镇子中,同一类的人数。
如果镇子中都是同一类人,那么收益就是1/2。如果是均等混合居住,那么收益最大。
最终的趋向就是,矮子都会在一个镇子,而高个子都在另外一个镇子中。这种现象是种族隔离现象。
纳什均衡点:
- 大家完全分开居住。是稳定的。
大家完全按照50%的比例进行混合居住。这是一种weak NE。并且这种纳什均衡是不稳定的,一旦镇子中有了变动,那么将会向另外一种纳什均衡移动。
所有人都选择一个镇子,然后进行随机分配。(lesson: 社会随机分配其结果要比主动选择好。多说一点,我居然找到我大学喜欢随机分配宿舍的理论解释了!太强大了!)
tipping point:一开始在一个纳什均衡点(50%-50%的状态),一旦有微小的变化,那么就会向另外一个纳什均衡点移动。
- 看似人们为了自己的利益,最终形成种族隔离。但是这样并不能推出人们更偏向于种族隔离(美国政治正确orz,实际上人们就是更偏向于种族隔离的)。
- 为了解决上面的问题,国家出台了一些政策:比如随机化,大家一起坐校车。
- 除了一种从上而下的随机,还有一种自下而上的随机,都是达到随机的目的。-> randomized or mixed strategy
例子
| 剪刀石头布游戏 | R | S | P |
|---|---|---|---|
| R | 0, 0 | 1, -1 | -1, 1 |
| S | -1, 1 | 0, 0 | 1, -1 |
| P | 1, -1 | -1, 1 | 0, 0 |
pure strategy = {R, S, P}。
这个博弈中没有pure纳什均衡点。
混合策略的纳什均衡点:(1/3, 1/3, 1/3)的概率进行游戏是纳什均衡点。
如果我出石头,payoff的期望=
同理可以计算出剪刀、布的期望都为0。
因此,该游戏
在纯策略的计算下,这是一个没有纳什均衡的游戏。但是一旦我们引入概率,那么剪刀石头布游戏就是一个有纳什均衡的游戏,这也是一个mixed strategy游戏。